Немного кассетной математики. Алгоритм работы счётчика дек Nakamichi.

ОООоооо … Я пишу о кассетниках ? По неявной просьбе antony1978
Тут ув. 2350 написал о некой диверсии от инженегров Nakamichi. А конкретнее — о том, что пробивает стабилизатор, питающий цифровую часть, что приводит к гибели процессоров (их там несколько) — дека "окирпичивается". Так что у кого "гром еще не грянул" — креститься не надо, лучше, почитайте и примите меры.
В данном случае повезло — основные процессоры (управления) остались живы, умерли отвечающие за лентяйку и счётчик.
Лентяйка, как и процессор управления мне не особо интересны. Скорее всего, их замена уже сделана умельцами. Если не сделана — предлагаю скооперироваться и сделать КиТ раскирпичивания дек Nakamichi (платку на Ардуине или чем похожем, Ардуина тут излишня т.к. аналоговая часть не будет задействована, любой не шибко умный микрокомпьютер или даже микропроцессор подойдёт).

Меня же заинтересовал алгоритм работы счётчика ленты. Ничего особо сложного. Третьеклассник, конечно, не справится, но и после 40 лет в это трудно "вкрутиться". Доказательство — то, что разговоры до сих пор идут, а сделано ли что-то, мне не ясно.

Мне это просто показалось интересной задачкой — мозги размять. Сюда пишу чтобы:
а) не забыть
б) мало ли кому это будет интересно или подтолкнет к более конкретным действиям, благо, спецов тут хватает.

Вводные данные: процессор получает сигналы с обоих катушек (импульсы), когда катушка проходит полный оборот. По этим данным надо определить, сколько ленты находится на одной и другой катушках. В распоряжении — только таймер. Изначальное количество ленты на катушках не известно, толщина ленты известна, но +/-, скорость вращения катушек — произвольная. Т.е. тоже определяется по таймеру по времени оборота.

Кстати, хорошая задачка для урока информатики в старших классах :-). Жизненно.

Вопрос 1: сколько ленты в метрах намотано на каждой катушке, если она сделала n оборотов от изначального ("голого") состояния?
Итак, немного математики:
dL = Pi*D; — Кол-во ленты, наматываемой на катушку за 1 оборот; D — диаметр катушки с лентой:
D = d + 2*n*h; d — диаметр голого ролика, n — количество слоёв намотанной плёнки (оборотов ролика от 0), h — толщина плёнки. 2 — понятно т.к. ДИАМЕТР катушки увеличивается на 2 толщины плёнки за 1 оборот.

Т.о. кол-во ленты на каждой катушке высчитывается как сумма длин за каждый оборот. Но сумму мы считать не будем, воспользуемся формулами интегрирования, благо, интеграл — суть та же самая сумма, только не дискретная, а непрерывная:
L = интеграл (dL*dn) = интеграл (Pi*D*dn) = интеграл Pi*(d + 2*n*h)dn = Pi*d*n + Pi*h*n^2 = Pi*(d+h*n)*n
L = Pi*(d+h*n)*n (1)
Эта формула нам потребуется в дальнейшем для расчёта того, сколько плёнки на каждой бобине в минутах или метрах.
n можно вычислить через L как корень соотв. квадратного уравнения ( n^2 + d/h*n — L/h/Pi = 0 ).

Вопрос 2: как определить, в каком месте кассеты мы находимся в данный момент?
Линейная скорость ленты пропорциональна диаметру катушки * ее угловую скорость. Угловая скорость пропорциональна 1/время оборота. Таким образом получаем:
dL = D1*w1 = D2*w2 (w1, w2 — угловые скорости бобин, w = 2*Pi/t, t — время оборота каждой бобины)
D1*w1 = D2*w2
2*Pi*D1/t1 = 2*Pi*D2/t2
D1/D2 = t1/t2
т.о. получили соотношение диаметров бобин и понимаем, в каком месте плёнки мы находимся. В процентах, долях, пропорции, … . Естественно, в реальных условиях нужна будет некая фильтрация, дабы данные "не скакали".
Попытаемся эти диаметры перевести в кол-во слоёв плёнки (оборотов каждой бобины):
D = d + 2*n*h (эта ф-ла была выше).
Дальше просто подставляем:
D1*t2 = D2*t1
(d + 2*n1*h)t2 = (d + 2*n2*h)t1
d*t2 + 2*h*n1*t2 = d*t1 + 2*h*n2*t1
d*(t2-t1) = 2*h*(n2*t1 — n1*t2)
n1*t2 — n2*t1 = d*(t1 — t2)/2/h
Немножко упростится, если подставить t2 = k*t1, k = t2/t1
n1*k*t1 — n2*t1 = d*(t1 — k*t1)/2/h
n2 — k*n1 = d/2/h*(k — 1)
n2 = k*n1 + d/2/h*(k — 1) (2)
Выразили одно через другое.

Есть еще 1 величина, связывающая n1 и n2. Это общая длина плёнки. Она тоже может быть разной, но от чего-то надо отталкиваться.
L = L1+L2 = Pi*d*(n1+n2)+Pi*h*(n1^2 + n2^2)
приведем к классическому виду (с коэф. 1 у второй степени)
n1^2 + n2^2 + d/h*(n1 + n2) — L/Pi/h = 0 (3)
подставляем сюда n2 = k*n1 + d/2/h*(k — 1), получаем квадратное уравнение, решение которого проходят в 8 классе (раньше в 7 проходили).

ПРИМЕР:
Допустим, у нас 90-минутная кассета.
толщина из справочника h = 0,012мм
Диаметр катка d = 22,4 мм
Длина ленты L = 135м или 135'000 мм

Например, времена 1 оборота бобин относятся как 1:1, т.е. на бобинах одинаково плёнки, k = 1.
n2 = k*n1 + d/2/h*(k — 1) = 1*n1+22,4/2/0,012*0 = n1 ( пока всё сходится :-) ).
n1^2 + n2^2 + d/h*(n1 + n2) — L/Pi/h = 0
n1^2 + d/h*n1 — L/Pi/h/2 = 0
n1^2 + 1866(6)*n1 — 1790493,109784 = 0
получились корни -2564.7757079669077 и 698.1090409669077. Отрицательный — сразу бракуем.
Т.е. какждая катушка — примерно 700 оборотов. Проверим.
L = Pi*(d+h*n)*n = Pi*(22,4+0,012*698)*698 = 67486,5875438 или 67,5 метров на каждой = 135м в сумме. Тут сошлось.

Пример 2: времена 1 оборота бобин относятся как 2:1, т.е. на 1 бобине много плёнки, на второй — меньше k = 2.
Поковыряюсь сначала в общем виде (жалко, спойлеров нет — не скрыть — проверять не обязательно)
n2 = k*n1 + d/2/h*(k — 1)
n1^2 + n2^2 + d/h*(n1 + n2) — L/Pi/h = 0
n1*(n1 + d/h) + n2*(n2 + d/h) — L/Pi/h = 0
n1*(n1 + d/h) + (k*n1 + d/2/h*(k — 1))*(k*n1 + d/2/h*(k — 1) + d/h) — L/Pi/h = 0
n1*(n1 + d/h) + (k*n1 + d/2/h*(k — 1))*(k*n1 + d/2/h*(k + 1)) — L/Pi/h = 0
n1^2 + d/h*n1 + k^2*n1^2 + k*n1*d/2/h*(k + 1) + k*n1*d/2/h*(k — 1) + d/2/h*(k — 1)*d/2/h*(k + 1) — L/Pi/h = 0
n1^2*(1 + k^2) + n1* (d/h + k*d/2/h*(k + 1) + k*d/2/h*(k — 1)) + d^2/4/h^2*(k^2 — 1) — L/Pi/h = 0
n1^2*(1 + k^2) + n1*d/h(1 + k^2) + d^2/4/h^2*(k^2 — 1) — L/Pi/h = 0, или
n1^2 + d/h*n1 + (d^2/4/h^2*(k^2 — 1) — L/Pi/h)/(1 + k^2) = 0
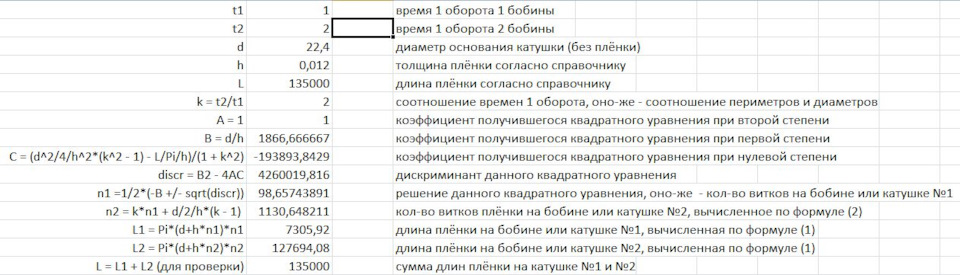
В сущности, вот наше квадратное уравнение — хоть в Эксель вставляй (пожалуй, так и сделаю).
Проверим c k=1: 2*n1^2 + 2*n1*d/h — L/Pi/h = 0 — вроде, не ошибся (см. пример с k=1).
С другими коэффициентами проще вбить табличку в Эксель с решением квадратного уравнения, что я и сделал.
k = 2: n1 = 99, n2 = 1130, L1 = 7306, L2 = 127694 Видно, что на бобине 1 ленты почти нет.

Файл тут

Вопрос 3. Как по времени оборота бобины вычислить толщину ленты?
Ну, естественно, надо смотреть, как изменяется это время с каждым оборотом бобины. Для этого надо знать и хранить в памяти несколько времён. Т.к. скорость той же перемотки не стабильна, надо смотреть обе бобины. На одной диаметр должен прирастать на 2 толщины ленты ленты с каждым ее оборотом, на второй — уменьшаться на такую же величину с каждым ее оборотом. Обороты разные. В общем, можно вычислить. Не хочу сейчас углубляться. Буду углубляться, только если будет конкретное задание/предложение.

Еще пришла в голову мысль, что по временам оборота обеих бобин, можно вообще вычислить общую длину ленты. Можно будет подумать об этом. Но опять-таки, если будет конкретный интерес. Вроде, это можно сделать, хоть точность будет не ахти.

Предполагаемый алгоритм работы счётчика такой:
Вставляем (вынимаем) кассету — всё сбрасывается на дефолты (величины из справочника).
Далее параллельно высчитываются:
— толщина плёнки по изменению времен оборотов — вносятся поправки к первоначальной величине. Поправки предварительно фильтруются.
— то, в каком месте кассеты мы находимся по соотношению времен оборотов.
— естественно, используются оптические датчики конца ленты.
Задача математически упрощается, если можно перемотать плёнку до начала, но будет странно, если аппарат будет это делать.

Еще раз, файл тут